双线性插值

参考博客：https://blog.csdn.net/qq_37577735/article/details/80041586

线性插值介绍

线性插值的几何意义即为概述图中利用过A点和B点的直线来近似表示原函数。线性插值可以用来近似代替原函数，也可以用来计算得到查表过程中表中没有的数值。

1）线性插值在一定允许误差下，可以近似代替原来函数； 2）在查询各种数值表时，可通过线性插值来得到表中没有的数值。

线性插值例子

题目： 给定两个点(x1, y1),(x2, y2)在中间x位置插值。

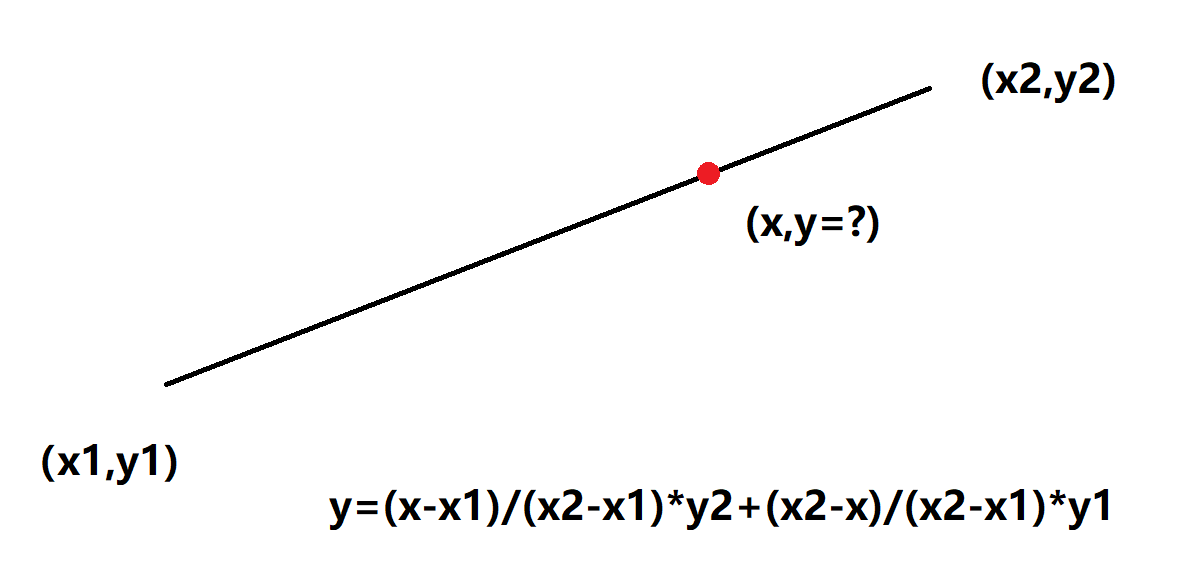
双线性插值法

在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。见下图：

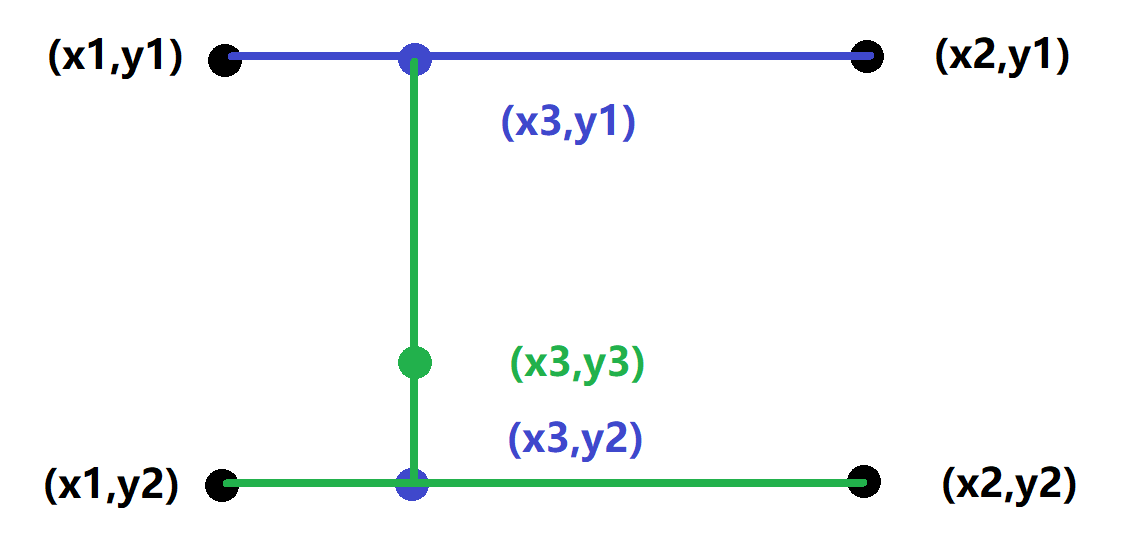
$$ f(x3,y1)=\frac{x2-x3}{x2-x1}f(x1,y1)+\frac{x3-x1}{x2-x1}f(x2,y1) $$

$$ f(x3,y2)=\frac{x2-x3}{x2-x1}f(x1,y2)+\frac{x3-x1}{x2-x1}f(x2,y2) $$

$$ f(x3,y3)=\frac{y3-y2}{y1-y2}f(x3,y1)+\frac{y1-y3}{y1-y2}f(x3,y2) $$