第六章 树形结构
6.1 树的基本概念
度:一个节点拥有的子节点数
树的度:所有节点度的最大值
森林:不相交的树构成的集合
6.3 树的存储结构
我觉得其实应该分为顺序存储,和链式存储
一个用数组,一个用链表
6.3.1 双亲表示法
struct node
{
int data;
int parent;
};
struct tree
{
node treeList[max_size];
int lenght;
};
6.3.2 孩子表示法
struct node
{
int data;
node *child[max_child];
};
6.3.3 兄弟表示法
struct node
{
int data;
struct node *left_child,*right_sibling;
};
6.4 树的遍历
前序遍历 根左右
中序遍历 左根右
后序遍历 左右根
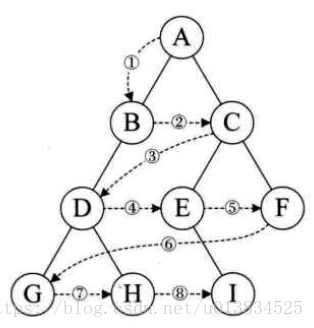
层次遍历
1 为什么叫前序、后序、中序?
一棵二叉树由根结点、左子树和右子树三部分组成,若规定 D、L、R 分别代表遍历根结点、遍历左子树、遍历右子树,则二叉树的遍历方式有 6 种:DLR、DRL、LDR、LRD、RDL、RLD。由于先遍历左子树和先遍历右子树在算法设计上没有本质区别,所以,只讨论三种方式:
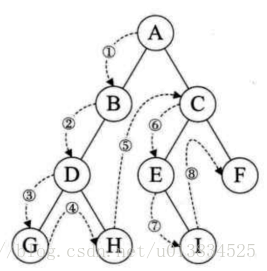
DLR--前序遍历(根在前,从左往右,一棵树的根永远在左子树前面,左子树又永远在右子树前面 )
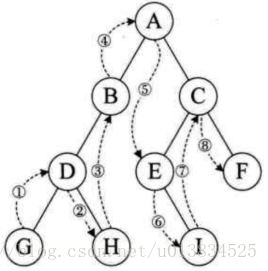
LDR--中序遍历(根在中,从左往右,一棵树的左子树永远在根前面,根永远在右子树前面)
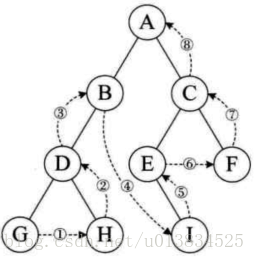
LRD--后序遍历(根在后,从左往右,一棵树的左子树永远在右子树前面,右子树永远在根前面)
参考博客:https://blog.csdn.net/u013834525/article/details/80421684
#include<iostream>
#include<vector>
#include<string>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include <stack>
#include<queue>
using namespace std;
struct node
{
char data;
node* left, * right;
};
void init_node(node* root, char data)
{
root->data = data;
root->left = nullptr;
root->right = nullptr;
}
void build_one_node_child(node* root, char* data, int left_child_no, int n)
{
if (left_child_no <= n && data[left_child_no] != ' ')
{
node* left_child = (node*)malloc(sizeof(node) * 1);
init_node(left_child, data[left_child_no]);
root->left = left_child;
build_one_node_child(left_child, data, left_child_no * 2, n);
}
int right_child_no = left_child_no + 1;
if (right_child_no <= n && data[right_child_no] != ' ')
{
node* right_child = (node*)malloc(sizeof(node) * 1);
init_node(right_child, data[right_child_no]);
root->right = right_child;
build_one_node_child(right_child, data, right_child_no * 2, n);
}
}
node* build_tree_from_layer(char* data, int n)
{
node* root = (node*)malloc(sizeof(node) * 1);
init_node(root, data[1]);
build_one_node_child(root, data, 2, n);
return root;
}
void display_pre(node *root)
{
if (root == nullptr)return;
printf("%c ", root->data);
display_pre(root->left);
display_pre(root->right);
}
void display_mid(node* root)
{
if (root == nullptr)return;
display_mid(root->left);
printf("%c ", root->data);
display_mid(root->right);
}
void display_post(node* root)
{
if (root == nullptr)return;
display_post(root->left);
display_post(root->right);
printf("%c ", root->data);
}
void display_layer(node* root)
{
queue<node*> node_queue;
node_queue.push(root);
int cnt = 0;
while(node_queue.size())
{
cnt = node_queue.size();
for (int i = 0; i != cnt; i++)
{
node* t = node_queue.front();
if (t->left != nullptr)node_queue.push(t->left);
if (t->right != nullptr)node_queue.push(t->right);
node_queue.pop();
printf("%c ", t->data);
}
printf("\n");
}
}
void destroy(node* root)
{
if (root->left != nullptr)destroy(root->left);
if (root->right != nullptr)destroy(root->right);
free(root);
root = nullptr;
}
int main()
{
char data[] = { ' ', 'A','B', 'C', 'D',' ', 'E', 'F', 'G', 'H',' ',' ',' ', 'I', ' ', ' '};
node *root= build_tree_from_layer(data, 15);
display_layer(root);
display_pre(root);
printf("\n");
display_mid(root);
printf("\n");
display_post(root);
printf("\n");
destroy(root);
return 0;
}
答案:
A
B C
D E F
G H I
A B D G H C E I F
G D H B A E I C F
G H D B I E F C A
6.5 树的线性表示
6.5.1 树的括号表示
A(B(D(G,H)), C(E(I),F))
这样就是括号表示,可以发现无法区分左右子节点,但允许一个节点下有多个子节点。
生成方式是前序遍历
6.5.2 树的层号表示
首先根据层号的定义为树中的每一个节点规定一个层号,然后按照前序遍历写出所有节点(带层号)。
1A 2B 3D 4G 4H 2C 3E 4I 3F