siamFC论文阅读

siamfc基本介绍

作者的siameseFC官网地址： http://www.robots.ox.ac.uk/~luca/siamese-fc.html

v1 版本的论文是原始版本，

v2 不清楚讲的啥。

v1

Fully-Convolutional Siamese Networks for Object Tracking

摘要

提出了一个全卷积的端到端的siamese网络，效果还不错。

1 介绍

我们认为视频目标跟踪目标的定义是视频第一帧给出的一个矩形框。

不啦不啦不啦

他们提倡仅仅训练一个学习相似度的深度学习网络，他们的主要贡献是证明了这种方法可行并且速度快。

特殊的，他们在目标图像的附近选择搜索区域，而不是把整个图像作为搜索区域。

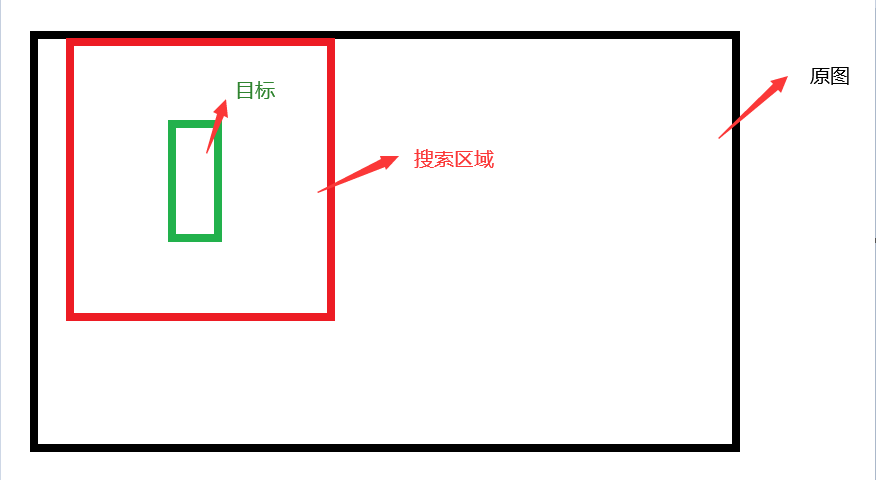
缩小搜索区域，大大降低了计算量，并且减少了目标跟踪发生大幅度漂移的情况，使跟踪更加稳定了。

进一步的贡献是提出一种新颖的全卷积的siamese网络结构：通过计算其两个输入的交叉相关的双线性层，实现了密集而有效的滑动窗口评估。

密集而有效是指他的anchor box的摆放很密集吗？

在我的毕设论文中也测试了，将原作者的密集摆放anchor变为平均摆放会使性能降低。

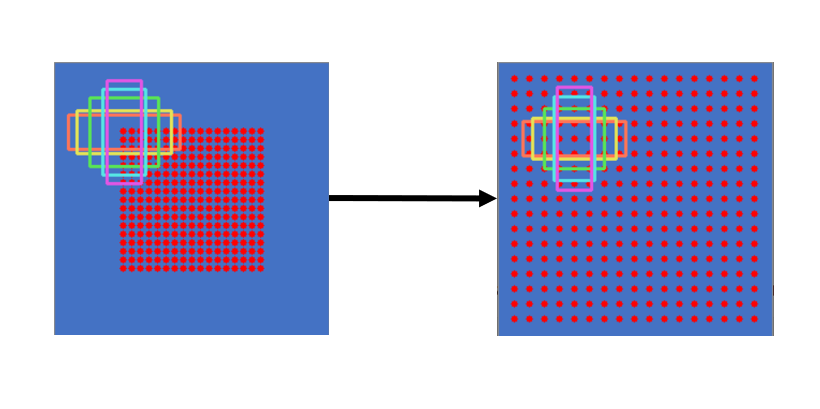
但是也可能是原作者为了降低计算量这么做的。

猜测：由于目标在相邻帧中的位移一般不会太大，在距离目标较远的位置检查意义不大，所以，将anchor密集的摆放在目标中间，可以提高跟踪位置的精度，而我将同样数量的anchor平均摆放，理论上可以注意到快速运动的目标，但是由于anchor不密集了，导致跟踪位置的精度降低。也许可以在整个搜素位置密集的摆放anchor，这样速度会降低，但是可以克服快速移动，但是如果周围同类目标较多，会不会引入额外的目标跟踪漂移呢？

2 Deep similarity learning for tracking

目标就是学习一个f(z,x),z是模板图像，x是候选图像，如果两个图像相似，就返回高分数，不相似就返回低分数。

为了找到目标的位置，我们就在所有候选区域，找到相似度最高的地方。

为了简单起见，我们只用视频第一帧给出的那个目标当作模板图像z。

模板的特征提取和候选区域的特征提取使用的同一个特征提取器，$\psi$,这个就是siamese的含义了，同一个，一模一样。

那么同一个目标提取出的特征理论上应该是比较相似的。

那么我们定义$\psi(x)$为提取获得的特征，那么我们还需要一个对比特征是否相似的一个函数$g(x)$.

这样f(z,x)就为：

$$ f(z,x) = g(\psi(z), \psi(x)) $$

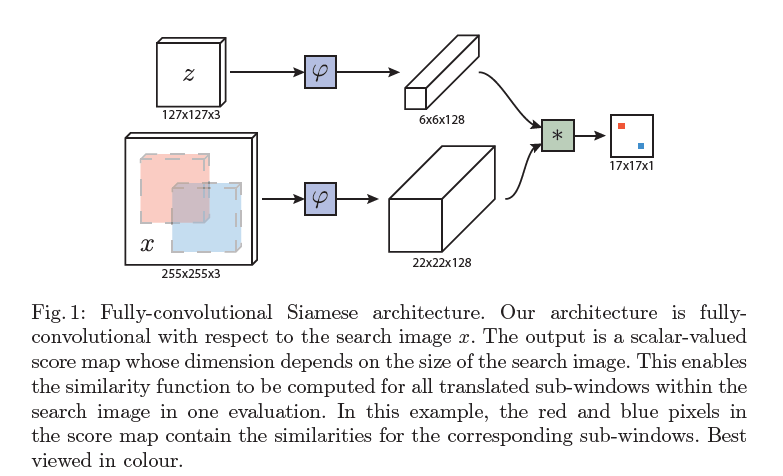
Fully-convolutional Siamese architecture

使用全卷积网络的好处是，不需要每次输入的图像大小相同，我们可以有更大的输入大小，并单一的评价每一个候选区域的子窗口与模板图像的相似度。

为了达到这个目的,我们使用一个卷积嵌入函数$\psi$,结合使用互相关层产生的特征图谱

$$ f(z,x) = \psi(z)*\psi(x)+b_1 $$

b 表示在每一个点的信号值，输出是一个score map，如上图1

每次下一帧的搜索区域定在上一帧的目标位置为中心的一个搜索区域。

Training with large search images

我们使用一个具有区别力的方法，使用正负样本，逻辑回归损失训练一个网络

$$ l(y,v)=log(1+exp((-yv))) $$

v是预测出的score，y是gt，$y\in{+1,-1}$

可以看出当时正样本的时候，y=1

当v->+无穷 那么l(y,v) -> 0

即正样本的时候预测的socre也应该越高，这样loss最小。

当v->-无穷 那么l(y,v)->+无穷

即正样本时，预测的score越低，loss就越大

当负样本时，y=-1

同理。

整个score map的loss定义为平均值：

$$ L(y,v) = \frac{1}{D}\sum_{u\in D}l(y[u],v[u]) $$

一对正样本是从同一个视频中不超过T帧提取的，

每幅图像在缩放时，是不改变图像的纵横比的。

score map的label，即那个y，到底是+1还是-1，是由那个点距离目标中心的距离决定的，如果距离小于等于半径R，那么就认为是正样本。否则认为是负样本。

k是网络的补偿

即：

$$ y[u]= \begin{cases} +1&if k||u-c|| \leq R\\ -1&otherwise \end{cases} $$

损失的正样本和负样本的例子在score map加权消除类别不平衡。

可以注意到，论文中的方法并没有在两个不同的视频中提取负样本，而仅仅根据简单的距离，来定义正负样本，也可以是说，iou大的地方就是正样本，iou小的地方就是负样本，毕竟搜索图像的大小是255 * 255，而模板图像的大小是127 * 127.

实验细节

模板图像的大小定为127 * 127，模板图像的大小定为255 * 255。

假设bbox的大小为（w，h），边缘补充的大小为p，s为放缩比例。

那么放缩公式如下：

$$ s(w+2p)*s(h+2p)=A $$

对于模板图像来说A=127*127

边缘补充的大小定义为p

$$ p=(w+h)/4 $$

即在原模板的bbox基础上，向外扩充一点。

有了这个公式，我们就可以知道我们应该裁剪多大了。

裁剪时如果我们裁剪模板，那么先根据(w,h)算出我们应该裁剪的正方形的大小（我们要保持图像的长宽比例，所以不能裁处图像后再放缩成正方形（因为网络输入需要正方形），再输入网络，而是应该直接裁剪对应大小的正方形，然后放缩到127 * 127）

那么假设要裁剪的正方形边长为square_size，那么计算公式如下：

$$ square_size = \sqrt{(w+2p)*(h+2p)} $$

代码为：

def calc_bounding_square_size(w, h):
    # context_amount = 0.5 这里的处理和siameseFC一致，算一个(w+2p)*(h+2p)=A^2
    context_amount = 0.5
    p_2 = (w + h)
    square_size = round(np.sqrt((w + context_amount * p_2) * (h + context_amount * p_2)))
    return square_size

还有一个就是关于anchor长宽比的设置为：

$$ 1.025^{[-2,-1,0,1,2]} $$

剩下的就是原作者的测试数据了。对比的算法也都比较老，意义不大。

v2：

题目： 基于相关过滤器的跟踪的端到端学习方法 End-to-end representation learning for Correlation Filter based tracking

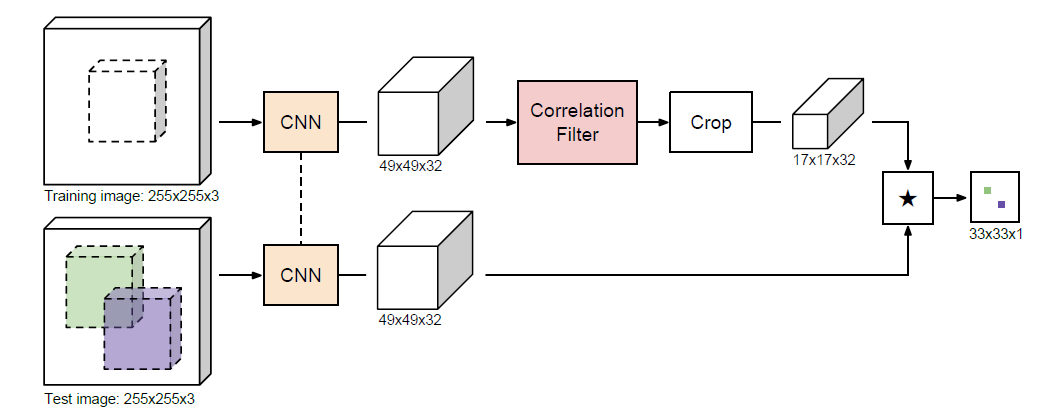
图1：建议的网络体系结构CFNet概述。 这是一个不对称的孪生网络：对两个输入图像应用相同的卷积特征变换后，“训练图像”用于学习线性模板，然后将其用于通过互相关搜索“测试图像”。

摘要： 相关滤波器是一种训练线性模板以区分图像及其平移的算法。 它非常适合对象跟踪，因为其在傅立叶域中的公式化提供了一种快速解决方案，使检测器每帧可以重新训练一次。 但是，以前使用“相关过滤器”的作品采用了手动设计或针对其他任务进行了培训的功能。 这项工作是通过将具有封闭形式的解决方案的“相关过滤器”学习器解释为深度神经网络中的一个可微层而克服此限制的第一项工作。 这样就可以学习与相关滤波器紧密耦合的深层功能。 实验表明，我们的方法具有重要的实际好处，即允许轻量级体系结构以高帧速率实现最新性能。

1 介绍

深度神经网络是在计算机视觉应用程序中学习图像表示的强大工具。 但是，为了从一个或几个示例中捕获以前看不见的对象类，在线培训深度网络具有挑战性。 这个问题自然出现在诸如视觉对象跟踪之类的应用中，其目的是在序列开始时仅在边界框的监督下重新检测视频上的对象。 主要挑战是缺乏对目标对象的先验知识，该知识可以是任何类别的。 最简单的方法是忽略先验知识的缺乏，并通过目标深层卷积神经网络（CNN）适应目标，例如通过使用随机梯度下降（SGD），即深度网络优化的主力[31， 25，35]。 极其有限的训练数据和大量参数使这成为一个困难的学习问题。 此外，SGD对于在线适应非常昂贵[31，25]。 这些缺点的可能答案是没有网络的在线适应。 最近的工作集中在学习可以用作通用对象描述符的深度嵌入[3，12，28，17，5]。 这些方法使用经过脱机训练的siameseCNN来区分两个图像块是否包含相同的对象。 想法是强大的嵌入将允许通过相似性检测（并由此跟踪）对象，从而绕开了在线学习问题。 但是，使用固定的指标比较外观会阻止学习算法利用任何可能有助于区分的视频特定提示。 一种替代策略是改用在线学习方法，例如“相关过滤器”（CF）。 CF是一种有效的算法，可通过极其有效地解决大型岭回归问题来学习将图像patch与周围的patch区分开来[4，13]。 事实证明，它在对象跟踪方面非常成功（例如[6、18、22、2]），其中，跟踪器的效率使跟踪器能够在每一帧动态调整对象的内部模型。 它的速度归因于傅立叶域公式化，这使得仅通过快速傅立叶变换（FFT）和廉价的按元素运算的少数应用即可解决岭回归问题。 通过设计，这种解决方案比像SGD这样的迭代求解器效率更高，并且与嵌入方法相反，仍允许区分器针对特定视频进行定制。 因此，挑战在于将CF的在线学习效率与离线训练的CNN功能的判别能力相结合。 这项工作已经在几项工作中完成（例如[21、7、9、31]），这些工作表明CNN和CF是互补的，并且它们的组合可以提高性能。 但是，在上述工作中，CF仅应用于预先训练的CNN特征之上，而没有对这两种方法进行任何深度集成。 相对于单独培训各个组件，通常更喜欢对深度架构进行端到端培训。 原因在于，以这种方式，所有组件中的自由参数都可以共同适应和协作以实现单个目标。 因此，很自然地问CNN-CF组合是否也可以具有相似的优势进行端到端的培训。 实现这种集成的关键步骤是将CF解释为可区分的CNN层，以便可以将错误通过CF传播回CNN功能。 这很具有挑战性，因为CF本身就是学习问题的解决方案。 因此，这需要区分大型线性方程组的解。 本文提供了相关过滤器导数的闭式表达式。 此外，我们展示了我们的方法在最终训练CNN架构方面的实用性。 我们目前对将CF合并到Bertinetto等人的全卷积暹罗框架中的效果进行了广泛的研究。 [3]。 我们发现，对于足够深的网络，CF不能改善结果。 但是，我们的方法可以使具有数千个参数的超轻量级网络在高帧速率下运行的同时，在多个基准上达到最新的性能。

2 相关工作

由于Bolme等人的开创性工作。 [4]，相关过滤器在跟踪社区中非常受欢迎。 值得注意的是，它已致力于改善它，例如通过减轻周期性边界的影响[10、15、8]，合并多分辨率特征图[21、9]并以更健壮的损耗来增强目标[26]。 为了简单起见，在这项工作中，我们采用相关滤波器的基本公式。 最近，已经引入了几种基于暹罗网络的方法[28、12、3]，由于其简单性和竞争优势，引起了跟踪社区的关注。 对于我们的方法，我们更喜欢在全卷积暹罗体系结构[3]的基础上构建，因为它强制执行了外观相似性函数应该与翻译互换的先验。 我们引入的相关性过滤器层的核心在于计算正则化反卷积问题的解决方案，不要与有时被称为“反卷积层”的上采样卷积层混淆[20]。 在发现诸如SGD之类的算法足以训练深度网络之前，Zeiler等人已经提出。 [34]介绍了一种深度架构，其中每一层都解决了卷积稀疏编码问题。 相反，由于相关滤波器采用二次正则化而不是1-范数正则化，因此我们的问题具有封闭形式的解决方案。 先前已经研究了在训练过程中通过对最优化问题的解进行反向传播梯度的想法。 Ionescu等。 [14]和Murray [24]分别提出了SVD和Cholesky分解的反向传播形式，使得梯度下降可以应用于网络，该网络可以计算线性方程组或特征值问题的解。 通过求解线性方程组（矩阵具有循环结构）的系统，可以将我们的工作理解为有效的反向传播过程。 当迭代获得优化问题的解决方案时，另一种方法是将迭代视为递归神经网络，并显式展开固定数量的迭代[36]。 Maclaurin等。文献[23]走得更远，并通过整个SGD学习过程进行反向传播梯度，尽管这在计算上要求很高，并且需要明智地记账。古尔德等。 [11]最近考虑将解决方案与一般的argmin问题区分开来，而并不局限于迭代程序。但是，对于相关过滤器来说，这些方法是不必要的，因为它具有封闭形式的解决方案。当迭代获得优化问题的解决方案时，另一种方法是将迭代视为递归神经网络，并明确展开固定数量的迭代[36]。 Maclaurin等。文献[23]走得更远，并通过整个SGD学习过程进行反向传播梯度，尽管这在计算上要求很高，并且需要明智地记账。古尔德等。 [11]最近考虑将解决方案与一般的argmin问题区分开来，而并不局限于迭代程序。但是，在相关滤波器的情况下，这些方法不是必需的，因为它具有封闭形式的解决方案。 通过学习算法进行反向传播会引发对元学习的比较。 最近的工作[30，1]提出了前馈体系结构，可以将其解释为学习算法，从而可以通过梯度下降进行优化。 本文没有采用抽象的学习定义，而是通过已经广泛使用的常规学习问题来传播梯度。

3 方法

在介绍CFNet架构（第3.3节）之前，我们简要介绍了一个siamese网络嵌入的框架（第3.1节）以及将这种嵌入用于对象跟踪（第3.2节）。 随后，我们导出了用于评估和反向传播网络中主要新成分的表达式，即相关过滤层，该层在前向执行在线学习（第3.4节）。

3.1. Fullyconvolutional Siamese networks

我们的起点是类似于[3]的网络，我们稍后对其进行了修改，以使模型可以解释为“相关过滤器”跟踪器。 全卷积暹罗框架考虑包括训练图像x'和测试图像z'1的对（x'，z'）。 图像x'代表感兴趣的对象（例如，在第一视频帧中以目标对象为中心的图像块），而z'通常更大，并且代表搜索区域（例如，下一视频帧）。

所有输入都经过一个有着一个可以学习的参数$\rho$的CNN$f_\rho$处理，这一层有两个特征图像。是一会儿用来做相关操作的。

eq1

$$ g_\rho(x', z') = f_\rho(x') * f_\rho(z') $$

等式1 的过程等同于在测试图像z'上进行模式x'的详尽搜索。 目标是使响应图的最大值（等式1的左侧）与目标位置相对应。 为了达到这个目的，网络使用了离线训练的方式，并且使用了几百万组($x'_i, z'_i$). 每个示例都有一个标签ci的空间图，标签的ci值为{-1，1}，真实对象位置属于正类别，所有其他对象均属于负类别。 在训练集上通过最小化元素级别的逻辑损失$\delta$来训练网络。

eq2

$$ arg\,\min_{\rho} \sum_{i}\delta(g_\rho(x'_i, z'_i), c_i) $$

3.2. Tracking algorithm

网络本身仅提供一种功能来测量两个图像块的相似性。 要将这个网络应用于对象跟踪，必须将其与描述跟踪器逻辑的过程结合起来。 类似于[3]，我们采用了一种简单的跟踪算法来评估相似度函数的效用。 通过简单地以正向模式评估网络即可执行在线跟踪。 将目标对象的特征表示与搜索区域的特征表示进行比较，该搜索区域是在每个新帧中通过提取以先前估计的位置为中心的窗口（面积为对象大小的四倍）而获得的。 对象的新位置被认为是得分最高的位置。 原始的全卷积暹罗网络仅将每个帧与对象的初始外观进行比较。 相反，我们在每个帧中计算一个新模板，然后将其与前一个模板合并在移动平均值中。

3.3. Correlation Filter networks

我们建议修改等式1标准的Siamese网络，通过在x和相关操作之间加上相关滤波块。 最终的架构如图1所示。此更改可以形式化为：

eq3

$$ h_{\rho,s,b}(x', z') = s\omega(f_\rho(x'))*f_\rho(z')+b $$

CF块w=w（x）通过解决傅立叶域中的岭回归问题，从训练特征图$x = f_\rho（x'）$计算出标准CF模板。 可以将其效果理解为精心制作具有针对翻译能力的区分模板。 必须引入标量参数s和b（比例和偏差）以使得分范围适合于逻辑回归。 然后，以与暹罗网络相同的方式执行离线训练（第3.1节），将等式2中的g替换为h.

我们发现，在训练图像中为关联过滤器提供较大范围的上下文非常重要，这与Danelljan等和Kiani等的发现是一致的。 为了减少圆形边界的影响，将特征图x预乘一个余弦窗口，并裁剪最终的模板。

请注意，图1中的体系结构的前向传递正好对应于具有CNN功能的标准CF跟踪器的操作，如先前的工作中所建议的。 但是，这些较早的网络没有经过端到端的培训。 新颖之处在于计算CF模板相对于其输入的导数，以便可以对端到端训练包含CF的网络。

3.4. Correlation Filter

现在，我们展示如何通过“相关过滤器”解决方案有效地反向传播梯度，并通过傅立叶域以封闭形式反向传播。

Formulation

$$ x \in R^{m*m} $$

$$ w \in R^{m*m} $$

给定标量值图像x,相关过滤器是模板w ，w是x和一个循环位移的图像的乘积，

$$ w=x*\delta_{-u} $$

这个乘积要尽可能的和期望的相应y[u]一致。 最小化：

eq4

$$ \sum_{u \in U}( < x * \delta_{-u}, w > - y[u])^2 =||w*x-y||^2 $$

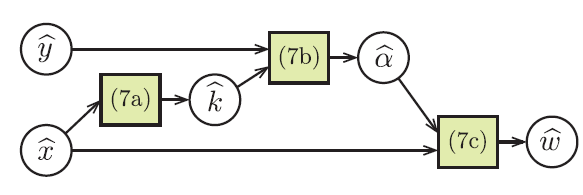
图2：相关滤波器的内部计算图。 方框表示在等式7中定义的函数，圆圈表示变量。

这里，U={0, ..., m-1}^2 是图像的空间域。

$y \in R^{mxm} $ 是第u个元素y[u]的标志，并且$\delta_r$是翻译过的Dirac delta函数 $\delta_r[t]=\delta[t-r]$。

在这一阶，我们使用*来代表循环卷积使用@表示循环相关。

回想那个使用了翻译过的$\delta$函数的卷积是和一下这个等价的$(x*\delta_r)[t]=x[t-r mod m]$.

纳入二次正则化以防止过度拟合，问题在于寻找

eq5

$$ arg\,\min_{w} \frac{1}{2n}||w@x-y||^2 + \frac{\lambda}{2}||w||^2 $$

n = |u|是样例的有效数量。

最佳模板w必须满足方程组（通过拉格朗日对偶获得，请参阅附录C，补充材料）

eq6

$$ k = \frac{1}{n}(x@x)+\lambda\delta $$ $$ k*\alpha = \frac{1}{n}y $$ $$ w = \alpha@x $$

其中k可以解释为定义循环线性核矩阵的信号，而α是由约束优化问题的拉格朗日乘数组成的信号，等效于eq 5.等式的解。 等式6可以在傅立叶域中有效地计算[13]，

$$ k $$