MOSSE论文阅读
Visual Object Tracking using Adaptive Correlation Filters
Abstract
本文介绍了一种新型的相关滤波器,即最小化平方误差和(MOSSE)滤波器,当使用单帧进行初始化时,该滤波器会产生稳定的相关滤波器。
基于MOSSE过滤器的跟踪器在以每秒669帧的速度运行时,可以抵抗光照,比例,姿势和非刚性变形的变化。
根据峰-旁瓣比率检测到遮挡,这使跟踪器可以暂停并在对象再次出现时从停止的位置继续。
1 Introduction
本文的其余部分安排如下。
第2节回顾了相关的相关滤波技术。
第3节介绍了MOSSE滤波器以及如何使用它创建基于鲁棒滤波器的跟踪器。
第4节介绍了来自[17]的七个视频序列的实验结果。
最后,第5节将回顾本文的主要发现。
2 Background
本文通过引入适用于视觉跟踪的ASEF规范化变体来减少训练图像需求。
3 Correlation Filter Based Tracking
基于过滤器的跟踪器使用在示例图像上训练的过滤器对对象的外观进行建模。
首先基于以第一帧中的对象为中心的小跟踪窗口选择目标。
从这一点开始,跟踪和过滤器训练将一起工作。
通过在下一帧的搜索窗口上关联过滤器来跟踪目标;相关输出中与最大值对应的位置指示目标的新位置。
然后基于该新位置执行在线更新。
要创建快速跟踪器,需要在傅立叶域快速傅立叶变换(FFT)中计算相关性。
首先计算输入图像的2D傅里叶变换$F = \mathcal F(f)$和滤波器的2D傅里叶变换$H = \mathcal F(h)$.
卷积定理指出,相关性在傅立叶域中变成了元素乘法。
使用⊙符号明确表示逐元素乘法,并使用*表示复共轭,相关性采用以下形式:
$$ G = F⊙H^* $$
使用逆FFT将相关输出转换回空间域。
此过程的瓶颈是计算正向和反向FFT,因此整个过程的上限时间为O(P log P),其中P是跟踪窗口中的像素数。
在本节中,我们讨论基于过滤器的跟踪器的组件。
3.1节讨论了在跟踪窗口上执行的预处理。
3.2节介绍了MOSSE滤波器,这是从少量图像构造稳定的相关滤波器的一种改进方法。
3.3节显示了如何使用正则化来生成更稳定的UMACE和ASEF过滤器。
3.4节讨论了用于过滤器在线更新的简单策略。
3.1 Preprocessing
FFT卷积算法的一个问题是图像和滤波器被映射到圆环的拓扑结构。
换句话说,它将图像的左边缘连接到右边缘,并将顶部连接到底部。
在卷积期间,图像旋转通过环形空间,而不是像在空间域中那样平移。
人工连接图像边界会引入影响相关输出的伪像。
通过遵循[3]中概述的预处理步骤,可以减少这种影响。
首先,使用对数功能对像素值进行转换,该功能有助于解决低对比度照明情况。
像素值被归一化为平均值为0.0,范数为1.0。
最终,将图像乘以余弦窗口,该余弦窗口将边缘附近的像素值逐渐减小为零。
这还有一个好处,就是可以将更多的重点放在目标的中心附近。
3.2 MOSSE Filters
MOSSE是一种用于从更少的训练图像中生成类似于ASEF的过滤器的算法。
首先,它需要一组训练图像fi和训练输出gi。
通常,gi可以采用任何形状。
在这种情况下,gi是由gt生成的,因此它具有一个紧凑的(σ= 2.0)2D高斯形状的峰值,该峰值以训练图像fi中的目标为中心。
训练在傅立叶域中进行,以利用输入和输出之间的简单元素关系。
如上一节所述,我们将大写变量Fi,Gi和过滤器H定义为它们的小写变量的傅立叶变换。
$$ H^*_i = \frac{G_i}{F_i} $$
这里的除法是逐元素的
为了找到一个将训练输入映射到所需训练输出的滤波器,MOSSE找到了一个滤波器H,该滤波器使卷积的实际输出与卷积的期望输出之间的平方误差之和最小。
此最小化问题的形式为:
(x是*,markdown又在搞事情)
$$ min_{H^x} \sum {|F_i ⊙ H^x-G_i|}^2 $$
将输出的平方误差和(SSE)最小化的想法并不新鲜。
实际上,等式3中的优化问题与[10]和[12]中提出的优化问题几乎相同。
不同之处在于,在那些作品中,假定目标始终始终以fi为中心,并且整个训练集的输出(gi)是固定的,而自定义每个gi是ASEF和MOSSE背后的基本思想。
在跟踪问题中,目标并不总是居中,并且gi中的峰值将跟随fi中的目标。
在更一般的情况下,gi可以具有任何形状。
例如,在[4]中,fi包含多个目标,而gi具有多个相应的峰。
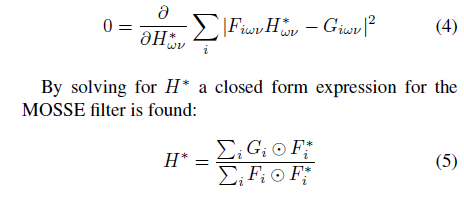
UMACE是MOSSE的一种特殊形式,它令$H^ = D^{-1}m^$了
3.3 Regularization of ASEF
ASEF采用略有不同的方法来最小化相关变换中的误差。
事实证明,当只有一个训练图像Fi和一个输出图像Gi时,存在一个产生零误差的滤波器。
该过滤器称为精确过滤器,可以通过求解找到
