DIMP论文阅读
Learning Discriminative Model Prediction for Tracking
Abstract
为了能够进行端到端的培训,目标模型的在线学习因此需要嵌入到跟踪体系结构本身中。
由于所施加的挑战,流行的siamese范例仅预测目标特征模板,而在推理过程中忽略了背景外观信息。
因此,预测模型具有有限的目标背景可分辨性。
我们开发了一种端到端的跟踪体系结构,能够充分利用目标和背景外观信息进行目标模型预测。
我们的体系结构是通过区分学习损失而设计的专用优化过程而产生的,该过程仅能在几次迭代中预测出强大的模型。
此外,我们的方法能够学习判别损失本身的关键方面。
项目地址:https://github.com/visionml/pytracking
1. Introduction

siamese的缺点:
1 首先,siamese跟踪器仅在推断模型时利用目标外观。这完全忽略了背景外观信息,这对于将目标与场景中的相似对象区分开来至关重要(请参见图1)。
2 其次,学习的相似性度量对于未包含在离线训练集中的对象不一定是可靠的,从而导致泛化不佳。
3 siamese方法没有提供强大的模型更新策略。
我们的方法:
1 我们采用基于最速下降法的方法来计算每次迭代中的最佳步长。
2 我们集成了一个模块,该模块可以有效地初始化目标模型。
我们的整个跟踪体系结构以及主干特征提取器,都通过使用带注释的跟踪序列,通过最大限度地减少了未来帧的预测误差来进行训练。
2. Related Work
siamese可以离线学习一个相似度判断,得到了较好的效果,但是忽略的对背景信息的利用。
另一系列的在线学习的算法,依赖于复杂的在线学习过程,较好利用了目标信息和背景信息。但无法进行端到端训练。
也有使用元学习使得在少量样本的情况下学习目标模板的方法。
3. Method
都是端到端训练,与Siamese不同,我们的体系结构可以充分利用背景信息,并提供自然而强大的手段来用新数据更新目标模型。
我们的模型预测网络源自两个主要原则:
(i)区分学习损失,促进学习目标模型的鲁棒性;
(ii)确保快速收敛的强大优化策略。
通过如此精心的设计,我们的架构仅需几次迭代就可以预测目标模型,而不会损害其判别能力。
在我们的框架中,目标模型构成卷积层的权重,提供目标分类得分作为输出。
我们的模型预测体系结构通过将一组带边界框注释的图像样本作为输入来计算这些权重。
模型预测器包括一个初始化器网络,该初始化器网络仅使用目标外观即可有效地提供模型权重的初始估计。
然后由优化程序模块处理这些权重,同时考虑目标和背景外观。
我们的最终跟踪架构由两个分支组成:一个目标分类分支(请参见图2),用于将目标与背景区分开;一个边界框估计分支,用于预测准确的目标框。
3.1. Discriminative Learning Loss
在本节中,我们将描述用于推导我们的模型预测架构的判别性学习损失。
我们的模型预测器 D 的输入包括一个训练集 $S_{train}={(x_j,c_j)}^n_{j=1}$ 深度特征图像 $x_j\in \mathcal X$ 是通过深度特征提取网络F获取的。
每个样本与对应的目标中心坐标配对 $c_j\in R^2$.
有了这些数据,我们的目标是预测一个目标模型$f=D(S_{train})$。
模型 f 被定义为卷积层的滤波器权重,其任务是区分特征空间$\mathcal X$ 中的目标和背景外观。
我们从基于最小二乘回归的跟踪问题中获得灵感,该问题近年来取得了巨大的成功 [6, 7, 15]。 然而,在这项工作中,我们概括了应用于多个方向跟踪的传统最小二乘损失,允许最终的跟踪网络从数据中学习最佳损失。
loss: $$ L(f) = \frac{1}{|S_{train}|} \sum_{(x, c)\in S_{train}} {||r(x*f, c)||}^2+{||\lambda f||}^2 $$
最常用的r的定义是:$r(s,c)=s-y_c$,$y_c$代表目标是否在那个位置的置信度。一般使用高斯函数生成模板相应图c。
但是,简单地取差值会迫使模型对所有负样本的校准置信度分数进行回归,通常为零。
这需要大量的模型容量,迫使学习专注于负数据样本,而不是实现最佳判别能力。
此外,采取天真的差异并没有解决目标和背景之间的数据不平衡问题。
为了缓解后面的数据不平衡问题,我们使用了空间权重函数$v_c$。
下标c表示对目标中心位置的依赖.
为了解决第一个问题,我们按照支持向量机的原理修改了损失。
我们在r中采用类似铰链(hinge-like loss)的损失,将背景区域中的分数s剪裁为零作为 max(0, s)。
因此,该模型可以自由地为背景中的简单样本预测大的负值,而不会增加损失。
另一方面,对于目标区域,我们发现添加类似的铰链损耗 max(0, 1-s) 是不利的。
虽然乍一看是矛盾的,但这种行为可归因于目标类和背景类之间的基本不对称,部分原因是数量不平衡。
此外,准确校准的目标置信度在跟踪场景中确实是有利的,例如用于检测目标丢失。
因此,我们需要目标邻域中标准最小二乘回归的特性。
为了兼顾最小二乘回归和铰链损失的优点,我们定义残差函数
$$ r(s, c) = v_c \cdot (m_cs+(1-m_c)max(0, s)-y_c) $$
目标区域定义为mask $m_c$.
对于每一个空间位置t,$t\in R^2$. $m_c(t) \in [0,1]$
同样,下标 c 表示对目标中心坐标的依赖。
公式能够根据图像相对于目标中心 c 的位置,不断地将损失的行为从标准最小二乘回归改变为铰链损失。
$m_c$在目标处的大小为1,越远离目标越小,在背景处的$m_c$为0.
然而,如何最佳设置 mc 尚不清楚,特别是在目标和背景之间的过渡区域。
虽然经典策略是使用反复试验手动设置掩码参数,但我们的端到端公式允许我们以数据驱动的方式学习mask $m_c$。
事实上,我们的方法学习了损失中的所有自由参数:目标掩码 $m_c$、空间权重 $v_c$、正则化因子$\lambda$,甚至回归目标 $y_c$ 本身。
3.2. Optimization Based Architecture
我们设计网络模型D,最小化损失,来预测滤波器f,$f = D(S_{train})$。
通过制定优化程序来设计网络。
我们有了上面的公式,就可以推导出面向滤波器f的loss$\nabla L$的梯度的封闭式表达。
直接的选择是使用步长 $\alpha$ 的梯度下降:
$$ f^{(i+1)} = f^{(i)}-\alpha \nabla L(f^{(i)}) $$
然而,我们发现这种简单的方法是不够的,即使学习率 $\alpha$(标量或系数特定)是由网络本身学习的(参见第 4.1 节)也是不够的。
它经历了滤波器参数 f 的缓慢适应,需要大量增加迭代次数。
这会损害效率并使离线学习复杂化。
梯度下降的缓慢收敛很大程度上是由于步长 $\alpha$ 不变,它不依赖于数据或当前模型估计。
我们通过推导更精细的优化方法来解决这个问题,只需要少量迭代即可预测强判别滤波器 f。
核心思想是基于最速下降法计算步长 $\alpha$,这是一种常见的优化技术。
我们首先用当前估计值 f^{(i)} 的二次函数近似损失:
$$ L(f) \approx \hat L(f) = \frac{1}{2}(f-f^{(i)})^TQ^{(i)}(f-f^{(i)})+(f-f^{(i)})^T\nabla L(f^{(i)})+L(f^{(i)}) $$
这里的f,$f^{(i)}$是向量,$Q^{(i)}$是正定的方阵。
然后最速下降法在梯度方向上寻找最佳步长$\alpha$来最小化上述的近似损失函数。
即令:
$$ \frac{d}{d\alpha}\hat L(f^{(i)}-\alpha \nabla L(f^{(i)})) = 0 $$
解得:
$$ \alpha = \frac{\nabla L(f^{(i)})^T\nabla L(f^{(i)})}{\nabla L(f^{(i)})^TQ^{(i)}\nabla L(f^{(i)})} $$
这个公式即是用于计算滤波器更新每次的迭代步长$\alpha$.
二次模型 (近似的loss) 以及由此产生的步长 (上述求解的$\alpha$) 取决于选择$Q^{(i)}$.
比如使用放缩的标识矩阵$Q^{(i)}=\frac{1}{\beta}I$
我们以固定步长$\alpha = \beta$来检索标准梯度下降算法。
另一方面,我们现在可以将二阶信息集成到优化过程中。
最明显的选择是为Hessian of the loss设置
$$ Q^{(i)} = \frac{\partial^2 L}{\partial f^2}(f^{(i)}) $$
这对应于二阶泰勒近似。
然而,对于我们的最小二乘公式 (1),高斯-牛顿方法提供了一种强大的替代方法,由于它只涉及一阶导数,因此具有显着的计算优势。
因此我们令:
$$ Q^{(i)} = (j^{(i)})^T(j^{(i)}) $$
其中 J(i) 是 f(i) 处残差的雅可比行列式。
事实上,矩阵 Q(i) 或 Jacobian J(i) 都不需要显式构造,而是作为一系列神经网络操作来实现。
算法 1 描述了我们的目标模型预测器 D。
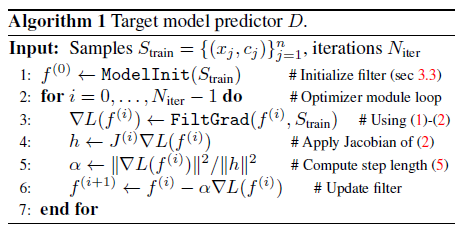
请注意,我们的优化器模块也可以轻松用于在线模型自适应。
这是通过使用来自先前跟踪帧的新样本不断扩展训练集 Strain 来实现的。
然后将优化器模块应用于此扩展训练集,使用当前目标模型作为初始化 f(0)。
3.3. Initial Filter Prediction
为了进一步减少 D 中所需的优化递归次数,我们引入了一个小网络模块来预测初始模型估计 f(0)。
我们的初始化网络由一个卷积层和一个精确的 ROI 池组成 。
后者从目标区域中提取特征并将它们汇集到与目标模型 f 相同的大小。
然后对 Strain 中的所有样本取平均池化特征图以获得初始模型 f(0)。
与 Siamese 跟踪器一样,这种方法仅利用目标外观。
然而,我们的初始化网络的任务不是预测最终模型,而是只提供合理的初始估计,然后由优化器模块处理以提供最终模型。
3.4. Learning the Discriminative Learning Loss
在这里,我们描述了定义损失 (1) 的残差函数 (2) 中的自由参数是如何学习的。
我们的残差函数包括标签置信度得分 $y_c$、空间权重函数 $v_c$ 和目标掩码 $m_c$。
虽然这些变量是在当前基于判别式在线学习的跟踪器中手工构建的,但我们的方法实际上是从数据中学习这些函数的。
我们根据与目标中心的距离对它们进行参数化。
这是由问题的径向对称性引起的,其中相对于目标的样本位置的方向意义不大。
相比之下,到样本位置的距离起着至关重要的作用,尤其是在从目标到背景的过渡中。
因此,我们使用径向基函数 $\rho_k$ 参数化 $y_c$、$m_c$ 和 $v_c$,并学习它们的置信度系数 $\phi_k$。
例如,位置 $t \in R^2$ 处的标签 $y_c$ 由下式给出:
$$ y_c(t) = \sum^{N-1}_{k=0} \phi^y_k \rho_k(||t-c||) $$
我们使用三角基函数 $\rho_k$,定义为:
$$ \rho_k(d)= \begin{cases} max(0, 1-\frac{|d-k\nabla|}{\nabla})& \text{k < N-1}\\ max(0, min(1, 1+\frac{d-k\nabla}{\nabla}))& \text{k = N-1} \end{cases} $$
上述公式对应于节点位移为 $\nabla$ 的连续分段线性函数。
请注意,最后一种情况 k = N-1 表示远离目标中心的所有位置,因此可以相同地处理。
我们使用一个小的 $nabla$ 来准确表示目标背景转换时的回归标签。
函数 $v_c$ 和 $m_c$ 在上面的$y_c(t)$ 的表达式中分别使用系数 $\phi^v_k$ 和 $\phi^m_k$ 类似地参数化。
我们使用sigmoid函数将$y_c(t)$的输出约束到[0,1]之间。
我们使用 N = 100 个基函数,并在深度特征空间 $\mathcal X$ 的分辨率下将结点位移设置为 $\nabla = 0.1$。
对于离线训练,回归标签 $y_c$ 被初始化为离线分类损失中使用的相同高斯 $z_c$。
权重函数 $v_c$ 被初始化为常数 $v_c(t) = 1$。
最后,我们使用缩放的 tanh 函数初始化目标掩码 $m_c$。
系数 $\phi_k$ 与 $\lambda$ 一起作为模型预测网络 D 的一部分学习。
y_c、m_c 和 v_c 的初始值和学习值在图 3 中可视化。
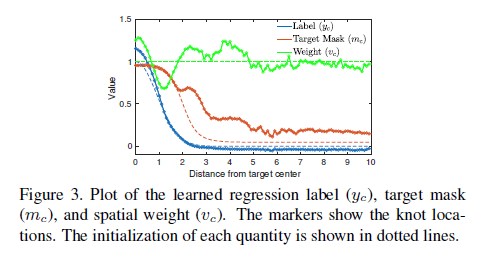
值得注意的是,我们的网络学习增加目标中心的权重 v_c,并在模糊过渡区域减少它。
3.5. Bounding Box Estimation
我们利用最大化overlap的策略来完成准确的边界框估计任务。
给定参考目标外观,训练边界框估计分支以预测目标与测试图像上的一组候选框之间的 IoU 重叠。
通过根据目标的参考外观计算调制向量,将目标信息集成到 IoU 预测中。
计算出的向量用于调制来自测试图像的特征,然后用于 IoU 预测。
IoU 预测网络是可微的 w.r.t.输入框坐标,允许在跟踪过程中通过最大化预测的 IoU 来优化候选者。
我们使用之前相同的网络架构。
3.6. Offline Training
在这里,我们描述了我们的离线训练程序。
在 Siamese 方法中,网络使用图像对进行训练,使用一个图像来预测目标模板,另一个用于评估跟踪器。
相比而言,我们的模型预测网络D的输入是一个集合$S_{train}$,包含序列中的多个样本数据。
为了更好的探索他的优势,我们在成对的训练集$(M_{train}, M_{test})$上训练我们完整的跟踪架构。
对于每一个M,$M = {(I_j,b_j)}^{N_{frames}}_{j=1}$.
其中$I_j$表述图像,$b_j$表示对应的bbox。
使用$M_{train}$来训练目标模型,使用$M_{test}$来评价。
独特的是,我们的训练允许模型预测器 D 学习如何更好地利用多个样本。
这些集合是通过对序列中长度为 $T_{ss}$ 的随机段进行采样来构建的。
然后我们通过分别从片段的前半部分和后半部分采样 $N_{frames}$ 帧来构建 $M_{train}$ 和 $M_{test}$。
给定对 $(M_{train},M_{test})$,我们首先将这些传给特征提取网络为我们的目标模型构造出来 $S_{train}$和 $S_{test}$ 的样本 。
$$ S_{train} = {(F(I_j), c_j):(I_j, b_j)\in M_{train}} $$
$c_j$代表$b_j$的邻域。
$$ f = D(S_{train}) $$
目的是预测模型 f 具有判别性并且可以很好地泛化到未来看不见的帧。
因此,我们仅在测试样本 $S_{test}$ 上评估预测模型 f,使用 $M_{test}$ 类似地获得。
我们使用背景样本的铰链计算回归误差:
$$ \iota (s,z)= \begin{cases} s-z& \text{z > T}\\ max(0, s)& \text{z <= T} \end{cases} $$
这里,阈值 T 基于标签置信度值 z 定义目标和背景区域。
对于目标区域 z > T,我们取预测的置信度分数 s 和标签 z 之间的差异,而我们只惩罚背景 z < T 的正置信度值。
总目标分类损失计算为所有测试样本的均方误差。
然而,我们不是仅评估最终目标模型 f,而是对优化器在每次迭代 i 中获得的估计 f(i) 的损失进行平均(参见算法 1)。
这为目标预测模块引入了中间监督,有利于训练收敛。
此外,我们的目标不是针对特定数量的递归进行训练,而是可以自由地在线设置所需的优化递归数量。
因此很自然地对每个迭代 f(i) 进行相等的评估。
用于离线训练的目标分类损失由下式给出,
$$ L_{cls} = \frac{1}{N_{iter}} \sum^{N_{iter}}{i=0} \sum, z_c)||^2 $$}} ||\iota (x*f^{(i)
这里,回归标签 $z_c$ 设置为以目标 c 为中心的高斯函数。
请注意,过滤器初始值设定项(第 3.3 节)的输出 f(0) 也包含在上述损失中。
虽然没有明确表示避免混乱,但上式中的 x 和 f(i) 都取决于特征提取网络 F 的参数。
模型迭代 f(i) 还取决于模型预测器网络 D 中的参数。
对于边界框估计,我们通过计算 $M_{train}$ 中第一帧的调制向量并从 $M_{test}$ 中的所有图像中采样候选框,将 ATOM 中的训练过程扩展到图像集。
边界框估计损失 $L_bb$ 计算为 $M_{test}$ 中预测的 IoU 重叠与地面实况之间的均方误差。
我们通过将其与目标分类损失(9)相结合来训练完整的跟踪架构作为 $L_{tot} = \beta L_{cls}+L_{bb}$
训练细节:
使用了TrackingNet[27], LaSOT [10], GOT10k [16] and COCO [24]datasets.
特征提取网络使用了ImageNet的权重进行初始化。
我们通过每个 epoch 采样 20,000 个视频来训练 50 个 epoch,在单个 Nvidia TITAN X GPU 上的总训练时间不到 24 小时。
我们使用 ADAM [19],每 15 个 epoch 的学习率衰减为 0.2。
目标分类损失权重$\beta = 10^2$.并且我们使用$N_{iter}=5$在优化器的迭代过程中。
(Mtrain;Mtest) 中的图像块是通过采样相对于目标注释的随机平移和比例来提取的。
我们将基本比例设置为目标大小的 5 倍以包含重要的背景信息。
对于每个序列,我们采样 Nframes = 3 个测试和训练帧,使用的段长度为 Tss = 60。
标签分数 z_c 是使用相对于基本目标大小的 1/4 的标准偏差构建的,我们使用 T = 0.05 为回归误差 (8)。
我们采用 ResNet 架构作为主干。
对于模型预测器 D,我们使用从第三个块中提取的特征,空间步长为 16。
我们将目标模型 f 的内核大小设置为 4 * 4。
3.7. Online Tracking
给定带有注释的第一帧,我们采用数据增强策略 [3] 来构建包含 15 个样本的初始集 Strain。
然后使用我们的判别模型预测架构 f = D(Strain) 获得目标模型。
对于第一帧,在初始化模块之后,我们采用了 10 次最速下降递归。
我们的方法允许通过向 Strain 添加新的训练样本来轻松更新目标模型,只要有足够的置信度预测目标。
我们通过丢弃最旧的样本来确保最大内存大小为 50。
在跟踪过程中,我们通过每 20 帧执行两次优化器递归或在检测到干扰峰时执行一次递归来优化目标模型 f。
使用与 [6] 中相同的设置执行边界框估计。