KCF论文阅读
High-Speed Tracking with Kernelized Correlation Filters
一个好的知乎链接:https://zhuanlan.zhihu.com/p/26685032
Abstract
大多数现代跟踪器的核心组件是区分性分类器,其任务是区分目标和周围环境。
为了应对自然图像变化,通常使用平移和缩放后的样本补丁来训练该分类器。
这样的样本集充满了冗余-任何重叠的像素都必须相同。(可能是说图像增强没啥用,还是同一个数据)
基于这个简单的观察,我们为成千上万个翻译补丁的数据集提出了一个分析模型。
通过显示结果数据矩阵是循环的,我们可以使用离散傅立叶变换对角化它,将存储和计算量减少几个数量级。
但是,对于内核回归,我们导出了一个新的内核相关过滤器(KCF),与其他内核算法不同,该算法与线性算法具有完全相同的复杂度。 在此基础上,我们还通过线性内核提出了线性相关滤波器的快速多通道扩展,我们称其为双相关滤波器(DCF)。
1 introduce
我们认为负采样不足是抑制跟踪性能的主要因素。
通过发现,在傅里叶域中,如果我们使用特定的模型进行翻译,随着我们添加更多样本,某些学习算法实际上会变得更加容易,这使得这成为可能。
这些分析工具,即循环矩阵,在流行的学习算法和经典信号处理之间架起了一座桥梁。
这意味着我们能够基于Kernel Ridge回归[8]提出一种跟踪器,该跟踪器不会遭受“核化的诅咒”,它的渐近复杂性更大,甚至比非结构化线性回归具有更低的复杂性。
相反,它可以看作是线性相关滤波器的内核版本,它构成了可用的最快跟踪器的基础[9],[10]。
我们的框架可以轻松地合并多个特征通道,并且通过使用线性内核,我们可以将线性相关滤波器快速扩展到多通道情况。
2 related work
2.1 On tracking-by-detection
2.2 On sample translations and correlation filtering
事实证明,相关滤波器在更复杂的方法上具有竞争优势,但是仅以一小部分的计算能力(每秒数百帧)使用。
他们利用了以下事实:两个patch的卷积(松散地,它们的点积在不同的相对平移下)等效于傅立叶域中的逐元素乘积。
因此,通过在傅立叶域中表述其目标,他们可以一次为多个平移或图像平移指定线性分类器的期望输出。
然而,由于在翻译图像,非线性内核和傅立叶域之间缺乏更清晰的关系,因此将内核技巧应用于其他过滤器已被证明更加困难[25],[24],其中一些建议需要明显更长的计算时间并具有强大的功能。
对我们来说,这暗示了翻译图像补丁和训练算法之间需要更深层次的联系,以克服直接傅立叶域公式化的局限性。
2.3 Subsequent work
自这项工作的最初版本[29]以来,提出的循环移位模型的一个有趣的时域变体已非常成功地用于视频事件检索[30]。
3 CONTRIBUTIONS
首次证明了具有循环移位样本的Ridge回归与经典相关滤波器之间的联系。
这样就可以使用O(n log n)快速傅立叶变换而不是昂贵的矩阵代数进行快速学习。
我们还将原始实验从12个视频扩展到了50个视频,并添加了新的Kernelized Correlation Filter(KCF)跟踪器变体,该跟踪器基于定向梯度直方图(HOG)功能而非原始像素。
通过线性内核,我们还提出了一种具有非常低的计算复杂度的线性多通道滤波器,该滤波器几乎可以与非线性内核的性能相匹配。
我们将其命名为双相关滤波器(DCF),并显示它与一组最近的,更昂贵的多通道滤波器之间的关系[31]。
通过实验,我们证明了KCF在没有任何特征提取的情况下已经比线性滤波器表现更好。
4 BUILDING BLOCKS
4.1 Linear regression
关注与Ridge Regression,因为他是一个简单的closed-form解决方法,闭环?,并且性能不错(和SVM对比)。
为了寻找一个合适的权重W
使得预测函数表现好:
$$ f(z)=w^Tz $$
就是最小化均方误差:
$$ \min_w\sum_i{(f(x_i)-y_i)}^2+\lambda||w||^2 $$
$\lambda$是一个正则化的参数,去防止过拟合
早期的方法最小化器是closed-form的,即:
$$ w = (X^TX+\lambda I)^{-1}X^Ty $$
X表示一行一个数据x_i的数据矩阵
y对应了X的每一行,都有一个y_i
I是一个单位矩阵
在傅里叶域,上边的式子化为:
$$ w = (X^HX+\lambda I)^{-1}X^Hy $$
就是转置变成了厄密共轭
通常,必须解决大型线性方程组以计算解决方案的情况,这在实时设置中可能会变得难以接受。
在接下来的段落中,我们将看到xi的一种特殊情况,它绕过了这一限制。

基本样本的垂直循环移位的示例。
我们的傅立叶域公式使我们可以对跟踪器进行基本样本的所有可能的循环移位,包括垂直和水平的循环移位,而无需明确地对其进行迭代。
可以看到环绕边缘的伪像(最左侧图像的顶部),但是余弦窗口和填充可以减轻这些伪像。
4.2 Cyclic shifts
为了简化符号,我们将重点介绍单通道一维信号。
这些结果以一种简单明了的方式推广到多通道二维图像(第7节)。
考虑一个n * 1的向量,该向量表示带有感兴趣对象的面片,表示为x。
我们将其称为基本样本。
我们的目标是训练带有基本样本(正面示例)和通过翻译获得的多个虚拟样本(作为负面示例)的分类器。
我们可以通过循环移位算子对此向量进行一维平移建模,这是置换矩阵
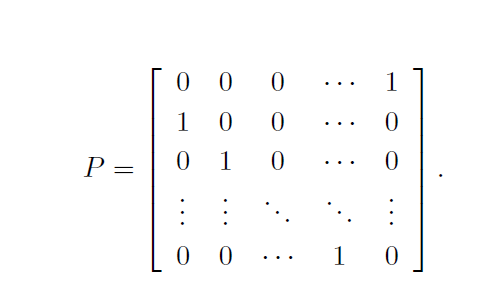
$$ X = [x_1, x_2, x_3, ..., x_{n-1}, x_n] $$
$$ PX = [x_n, x_1, x_2, x_3, ..., x_n-1]^T $$
我们可以使用$P^uX$,获得更大的平移。
-u可以反方向平移
同理竖直方向也可以循环平移
循环n次就是一轮,所以整个集合可以看作:
$$ {P^uX|u=0, 1, ..., n-1} $$
同样,由于具有循环特性,我们可以等效地将此集合的前半部分视为正向移动,而将后半部分视为负向移动
4.3 Circulant matrices
我们可以把一个样本X的n种循环搞在一起,形成一个n * n的矩阵
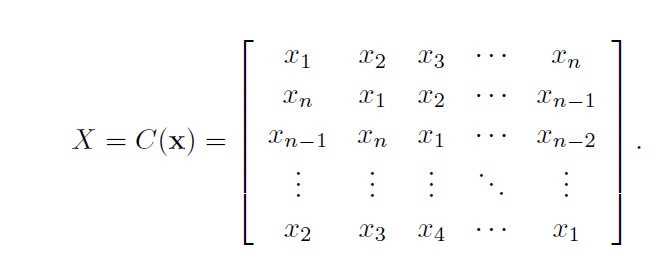
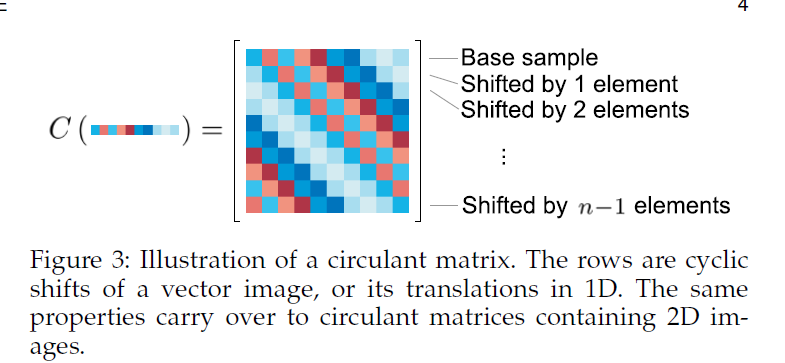
彩色的颜色图表示如下图:
也许最令人惊讶和有用的事实是,不管生成矢量x是什么,所有循环矩阵都通过离散傅立叶变换(DFT)做成对角线。 这可以表示为
$$ X = F diag(\hat X)F^H $$
F是一个不依赖与X的常数矩阵,$\hat X$表示x的DFT(离散傅里叶变换)变换结果。
$$ \hat X = \mathcal F(x) $$
之后我们把带^的变量作为DFT变化后的结果
F这个常量矩阵,称为DFT matrix。对于所有输入的x,这个矩阵都是同一个
$$ \mathcal F(z) = \sqrt{(n)}FZ $$
这个等式是因为离散傅里叶变化是线性操作。
4.4 Putting it all together
现在我们可以使用现有知识去简化
$$ w = (X^HX+\lambda I)^{-1}X^Hy $$
当训练数据是由循环位移组成的话。
能够仅仅使用对角矩阵是十分具有吸引力的,以为所有的操作都可以在对角元素上对于元素进行(矩阵的对应位置相乘)。
采取术语$X^HX$,可以将其视为非中心协方差矩阵。
代入下式
$$ X = F diag(\hat X)F^H $$
得到
$$ X^HX = Fdiag(({\hat x}^*)F^HFdiag(\hat x)F^H $$
由于对角矩阵是对称的,因此仅将Hermitian转置为复共轭 ${\hat x}^*$
此外,我们可以消除因子$F^HF=I$
得到:
$$ X^HX = Fdiag({\hat x}^*)diag(\hat x)F^H $$
定义element-wise product,即矩阵的对应位置相乘,为$\bigodot$
由于对角矩阵可化为
$$ X^HX = Fdiag({\hat x}^*\bigodot {\hat x})F^H $$
一个有趣的方面是,括号中的矢量被称为信号x的自相关(在傅立叶域中,也称为功率谱[21])。 在经典信号处理中,它包含随时间变化的时差变化,对于不同的时滞,在我们的情况下是空间。 上面的步骤总结了用循环矩阵对角化表达式时所采用的一般方法。 将它们递归地应用于线性回归的完整表达式(等式3),我们可以将大多数数量放在对角线内,
$$ \hat w = diag(\frac{{\hat x}^}{{\hat x}^ \bigodot {\hat x}+\lambda}){\hat y} $$
或者
$$ \hat w = \frac{{\hat x}^ \bigodot {\hat y}}{{\hat x}^ \bigodot {\hat x}+\lambda} $$
我们可以使用逆DFT在空间域中轻松恢复w,其成本与前向DFT相同。