FFT

FFT(Fast Fourier Transform)

快速傅里叶变换

用于加速两个多项式的乘积。

在ACM中那就是大整数乘法的加速

$$ O(n^2)->O(nlogn) $$

思路

用系数表示法相乘两个多项式，复杂度是O(n^2).

但是用点值表示法相乘，复杂度是O(n)

快速傅里叶变换，就是考虑，先将多项式由系数表示法转化为点值表示法，点值表示法相乘后，再转换为系数表示法。

多项式的表示

n个点可以唯一表示一个n-1次多项式

系数表示法：

$$ f(x) = a_0 + a_1x_1+a_2x_2+ ... +a_{n-1}x_{n-1} $$

点值表示法：

$$ f(x) = {(x_0, y_0), (x_1, y_1), ..., (x_{n-1}, y_{n-1})} $$

点值表示法的相乘，就是对应x的y相乘，得到新的y

$$ f^a(x) = {(x_0, y^a_0), (x_1, y^a_1), ..., (x_{n-1}, y^a_{n-1})} $$

$$ f^b(x) = {(x_0, y^b_0), (x_1, y^b_1), ..., (x_{n-1}, y^b_{n-1})} $$

$$ f^a(x) * f^b(x) = {(x_0, y^a_0 * y^b_0), (x_1,y^a_1* y^b_1), ..., (x_{n-1}, y^a_{n-1} * y^b_{n-1})} $$

DFT

DFT(Discrete Fourier Transform)

离散傅里叶变换要解决：

加速 系数表示法 -> 点值表示法

$$ a = (a_0, a_1, a_2, ..., a_{n-1}) -> (x, y) = ((x_0, y_0), (x_1, y_1), ..., (x_{n-1}, y_{n-1})) $$

普通来说，一个n-1次多项式，我们只需要随便取n个不同的x，计算出来n个对应的f(x),就可以得到点值表示法了。

但是这样，要算n次f(x),每次计算中间又有n次乘法。整体复杂度是O(n^2)的

由一个x计算一个f(x)这一步，需要计算$1, x, x^2, x^3, ..., x^{n-1}$这些计算可以用分治的方法加速。

$$ f(x) = a_0 + a_1x_1+a_2x_2+ ... +a_{n-1}x_{n-1} $$

若想使用分治，那么就将所有多项式用系数0，补成一个2的次幂的项数的多项式，

比如:

$$ f(x) = 1 + x + x^2 $$

补成：

$$ f(x) = 1 + x + x^2 +0*x^3 $$

按照奇偶分开得到：

$$ \begin{aligned} f(x) &= (a_0+a_2x^2+...+a_{n-2}x^{n-2}) + (a_1x+a_3x^3+...+a_{n-1}x^{n-1})\\ &= (a_0+a_2x^2+...+a_{n-2}x^{n-2}) + x(a_1+a_3x^2+...+a_{n-2}x^{n-2}) \end{aligned} $$

容易发现这是一个递归的分治优化。

n次单位根

欧拉公式：

$$ cosx = 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}... $$

$$ sinx = x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}... $$

$$ e^x = 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}... $$

易得：

$$ e^{ix} = cosx+isinx $$

$$ e^{i\theta} = cos\theta+isin\theta $$

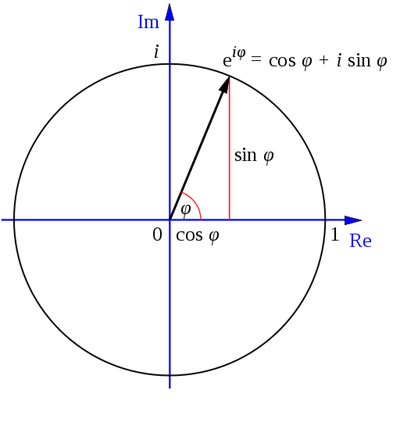
n次单位根:

$$ \omega_n $$

$$ \omega_n^n = 1 $$

$$ \omega_n^{n+m} = \omega^m $$

$$ {(\omega_n^m)}^n = {(\omega_n^n)}^m = 1 $$

1开n次方的答案：

相当于把那个圆分n份，$\omega_n$是一份的大小，$\omega_n^m$就是m份大小

$$ \omega_n = e^{\theta\frac{2\pi}{n}} $$

$$ \omega_{2n}^{2i} = \omega_n^{i} $$

$$ \omega_n^{i} = -\omega_n^{i+n/2} $$

$$ {(\omega_n^{i})}^2 = -\omega_n^{2i} = -\omega_{n/2}^{i} $$

$$ \sum_{i=0}^{n-1} \omega^{ik}_n = \begin{cases} 0& k \% n \neq 0 \\ n& k \% n = 0 \end{cases} $$

上面的写法可能不好看出来，下面这个公式容易看出来：

markdown的问题，下面的$\omega$代表$\omega_n$，即n次单位根

$$ 1+\omega^k+\omega^{2k}+\omega^{3k}+...+\omega^{(n-1)k} = \begin{cases} 0& k \% n \neq 0 \\ n& k \% n = 0 \end{cases} $$

可知当k是n的倍数的时候：

$$ \omega^{ik} = \omega^{in*(k/n)} = 1 $$

所以：

$$ 1+\omega^k+\omega^{2k}+\omega^{3k}+...+\omega^{(n-1)k} = 1+1+1+1+1+...+1 = n $$

当k不是n的倍数的时候：

$$ \omega^{ik} \neq 1 $$

$$ 1-\omega^{ik} \neq 0 $$

才有下式：

$$ \sum^{n-1}_{i=0} \omega^{ik} = \frac{\omega^k(1-{(\omega^{k})}^n)}{1-\omega^{k}} = 0 $$

IDFT

IDFT(Inverse Discrete Fourier Transform)

离散傅里叶逆变换

$$ (x, y) = ((x_0, y_0), (x_1, y_1), ..., (x_n, y_n)) -> a = (a_0, a_1, a_2, ..., a_n) $$

不行了，想不明白，太难了

留下代码做个纪念吧：

fft是真正的板子

DFT_0是最朴素的DFT

DFT_1是加速了的

DFT_2是递归版的

DFT_3是试图自己写的递归转动规，失败了，感觉没有理解这个算法，复现不了

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<cmath>
#include<vector>
using namespace std;
const int MAXN = 30;
inline int read()
{
    char c = getchar(); int x = 0, f = 1;
    while (c < '0' || c>'9') { if (c == '-')f = -1; c = getchar(); }
    while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}
const double Pi = acos(-1.0);
struct complex
{
    double x, y;
    complex(double xx = 0, double yy = 0) { x = xx, y = yy; }
}a[MAXN];
complex operator + (const complex &a, const complex &b) { return complex(a.x + b.x, a.y + b.y); }
complex operator - (const complex &a, const complex &b) { return complex(a.x - b.x, a.y - b.y); }
complex operator * (const complex &a, const complex &b) { return complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x); }//不懂的看复数的运算那部分 
ostream& operator << (ostream& out, const complex& a) { out << a.x << " " << a.y; return out; }
int n;
int order[MAXN];
int cnt = 0;
int limit = 1;

void o()
{
    cout << "o:" << endl;
    for (int i = 0; i != limit; i++)
    {
        cout << a[i] << " ";
    }
    cout << endl;
}

void refine()
{
    for (int i = 0; i != limit; i++)
    {
        a[i].x = int(a[i].x / limit + 0.5);
    }
}

void fast_fast_tle(complex* A, int type)
{
    for (int i = 0; i < limit; i++)
        if (i < order[i]) swap(A[i], A[order[i]]);//求出要迭代的序列 
    for (int mid = 1; mid < limit; mid <<= 1)//待合并区间的中点
    {
        complex Wn(cos(Pi / mid), type * sin(Pi / mid)); //单位根 
        for (int R = mid << 1, j = 0; j < limit; j += R)//R是区间的右端点，j表示前已经到哪个位置了 
        {
            complex w(1, 0);//幂 
            for (int k = 0; k < mid; k++, w = w * Wn)//枚举左半部分 
            {
                //cout << j + k << " " << j + mid + k << endl;
                //cout << order[j + k] << " " << order[j + mid + k] << endl;
                if(type>0)
                cout << "c: " << order[j + k] << " " << order[j + mid + k] << " " << 2 * mid << " " << k << endl;
                complex x = A[j + k], y = w * A[j + mid + k];//蝴蝶效应 
                A[j + k] = x + y;
                A[j + mid + k] = x - y;
            }
        }
    }
}

void fast_fast_tle2(int limit, complex* a, int type)
{
    if (limit == 1) return;//只有一个常数项
    const int sub_len = limit/2;
    complex *a1, *a2;
    a1 = (complex *)malloc(sub_len*sizeof(complex));
    a2 = (complex *)malloc(sub_len*sizeof(complex));
    for (int i = 0; i < limit; i += 2)//根据下标的奇偶性分类
        a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
    fast_fast_tle2(sub_len, a1, type);
    fast_fast_tle2(sub_len, a2, type);
    complex Wn = complex(cos(2.0 * Pi / limit), type * sin(2.0 * Pi / limit)), w = complex(1, 0);
    //Wn为单位根，w表示幂
    for (int i = 0; i < (limit >> 1); i++, w = w * Wn)//这里的w相当于公式中的k 
    {
        complex x = a1[i], y = w * a2[i];//蝴蝶效应 
        a[i] = x + y;
        a[i + (limit >> 1)] = x - y;//利用单位根的性质，O(1)得到另一部分 
    }
    free(a1);
    free(a2);
}

void fast_fast_tle3(int limit, complex* a, int type)
{
    if (limit == 1)return;
    complex x, y;
    complex al[10], ar[10];
    int sub_len = limit / 2;
    for (int i = 0; i != sub_len; i++)
    {
        cout << i << endl;
        al[i] = a[i * 2];
        ar[i] = a[i * 2 + 1];
    }
    fast_fast_tle3(sub_len, al, type);
    fast_fast_tle3(sub_len, ar, type);
    complex w(1, 0);
    complex wn(cos(2.0 * Pi / limit), type * sin(2.0 * Pi / limit));
    for (int i = 0; i != sub_len; i++)
    {
        x = al[i];
        y = w * ar[i];
        a[i] = x + y;
        a[i + limit / 2] = x - y;
        w = w * wn;
    }
}

void read_data()
{
    n = read();
    for (int i = 0; i <= n; i++) a[i].x = read();
}

void build_order()
{
    for (int i = 0; i < limit; i++)
        order[i] = (order[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
    //for (int i = 0; i < limit; i++)
    //    cout << order[i] << " ";
    //cout << endl;
}

void DFT_0(int limit, complex *a, int type)
{
    vector<complex> copy_a;
    for (int i = 0; i != limit; i++)
    {
        copy_a.push_back(a[i]);
    }

    for (int i = 0; i != limit; i++)
    {
        complex w(1, 0);
        complex wn(cos((2 * Pi / limit) * i), type * sin((2 * Pi / limit) * i));
        a[i] = complex(0, 0);
        for (int j = 0; j != limit; j++)
        {
            a[i] = a[i] + w * copy_a[j];
            w = w * wn;
        }
    }
}

void DFT_1(int limit, complex* a, int type)
{
    // 优化A(w_i+n/2)的计算
    int sub_limit = limit / 2;
    complex* a_left = (complex*)malloc(sub_limit * sizeof(complex));
    complex* a_right = (complex*)malloc(sub_limit * sizeof(complex));

    for (int i = 0; i != limit / 2; i++)
    {
        a_left[i] = a[i * 2];
        a_right[i] = a[i * 2 + 1];
    }

    for (int i = 0; i != limit / 2; i++)
    {
        complex x, y;
        complex w(1, 0);
        complex wn(cos((2 * Pi / limit) * i), type * sin((2 * Pi / limit) * i));
        complex wn2(cos((2 * Pi / sub_limit) * i), type * sin((2 * Pi / sub_limit) * i));
        for (int j = 0; j != sub_limit; j++)
        {
            x = x + w * a_left[j];
            y = y + w * a_right[j];
            w = w * wn2;
        }
        y = wn * y;
        a[i] = x + y;
        a[i + limit / 2] = x - y;
    }

    free(a_left);
    free(a_right);
}

void DFT_2(int limit, complex* a, int type)
{
    // 优化A(w_i+n/2)的计算
    if (limit == 1)return;
    int sub_limit = limit / 2;
    complex* a_left = (complex*)malloc(sub_limit * sizeof(complex));
    complex* a_right = (complex*)malloc(sub_limit * sizeof(complex));

    for (int i = 0; i != limit / 2; i++)
    {
        a_left[i] = a[i * 2];
        a_right[i] = a[i * 2 + 1];
    }

    DFT_2(sub_limit, a_left, type);
    DFT_2(sub_limit, a_right, type);

    complex w(1, 0);
    complex wn(cos(2 * Pi / limit), type * sin(2 * Pi / limit));
    for (int i = 0; i != limit / 2; i++)
    {
        cout<<"c: "<<limit<<" "<<i<<endl;
        complex x, y;
        x = a_left[i];
        y = w * a_right[i];
        a[i] = x + y;
        a[i + limit / 2] = x - y;
        w = w * wn;
    }
    free(a_left);
    free(a_right);
}

void DFT_3(int limit, complex* a, int type)
{
    //递归转动规
    int layer = cnt;
    int out_loop = (limit + 1) / 2;
    int in_loop = 1;
    for (int i = 0; i != layer; i++)
    {
        for (int j = 0; j != out_loop; j++)
        {
            for (int k = 0; k != in_loop; k++)
            {
                double theta = 2 * Pi / (in_loop * 2) * k * out_loop;
                complex wn(cos(theta), type * sin(theta));
                int no1 = j + k * out_loop * 2, no2 = j + out_loop + k * out_loop * 2;
                cout << "c: " << no1 << " " << no2 << " by: " << (in_loop * 2) <<" "<< k * out_loop << endl;
                complex x = a[no1], y = wn * a[no2];
                a[no1] = x + y;
                a[no2] = x - y;
            }
        }
        out_loop /= 2;
        in_loop *= 2;
    }
}

void resume(int limit, int group_size, int *my_order)
{
    vector<int> new_order;
    for(int i=0;i!=limit/group_size/2;i++)
    {
        for(int j=0;j!=group_size;j++)
        {
            int no1,no2;
            no1 = (i*2)*group_size+j;
            no2 = (i*2+1)*group_size+j;
//          cout<<"no1: "<<no1<<" no2: "<<no2<<endl;
            new_order.push_back(my_order[no1]);
            new_order.push_back(my_order[no2]);
        }
    }
    for(int i=0;i!=limit;i++)
    {
        my_order[i] = new_order[i];
    }
//  cout<<"myorder"<<endl;
//  for(int i=0;i!=limit;i++)
//  {
//      cout<<my_order[i]<<" ";
//  }
//  cout<<endl;
}

void DFT_4(int limit, complex* a, int type)
{
    //递归转动规
    int *my_order = (int *)malloc(limit);
    for (int i = 0; i < limit; i++)
        my_order[i] = (my_order[i >> 1] >> 1) | ((i & 1) << (cnt - 1));

    int layer = cnt;
    int out_loop = limit / 2;
    int in_loop = 1;
    for (int i = 0; i != layer; i++)
    {
        for(int p=0;p!=out_loop;p++)
        {
            for(int q=0;q!=in_loop;q++)
            {
                double theta = 2*Pi/(in_loop*2)*q;
                complex wn(cos(theta), type*sin(theta));        
                complex x,y;
                int no1, no2;
                no1 = p*(in_loop*2)+q*2;
                no2 = no1+1;

//              cout<<"cz: "<<no1<<" "<<no2<<endl;

                no1 = my_order[no1];
                no2 = my_order[no2];

                cout<<"c: "<<no1<<" "<<no2<<" "<<(in_loop*2)<<" "<<q<<endl;


                x = a[no1];
                y = wn*a[no2];
                a[no1] = x+y;
                a[no2] = x-y;
            }
        }
        out_loop/=2;
        in_loop*=2;
        if(i+1!=layer)
            resume(limit, in_loop, my_order);
    }
}

void DFT_5(int limit, complex* a, int type)
{
    //递归转动规
    int *my_order = (int *)malloc(limit);
    for (int i = 0; i < limit; i++)
        my_order[i] = (my_order[i >> 1] >> 1) | ((i & 1) << (cnt - 1));


}

int main()
{
    freopen("D:/c++/dev/in.txt", "r", stdin);
    read_data();
    while (limit <= n) limit <<= 1, cnt++;
    build_order();

    // 在原序列中 i 与 i/2 的关系是 ： i可以看做是i/2的二进制上的每一位左移一位得来
    // 那么在反转后的数组中就需要右移一位，同时特殊处理一下复数 

    //o();
//    fast_fast_tle(a, 1);
//    o();
//    fast_fast_tle(a, -1);
    //o();

    DFT_1(limit, a, 1);
    o();
    DFT_1(limit, a, -1);

    refine();
    //o();
//    fast_fast_tle3(limit, a, 1);
//    DFT_2(limit, a, 1);
//  fast_fast_tle2(limit, a, 1);
//    o();
//    DFT_2(limit, a, -1);
//    refine();
//    o();
    DFT_4(limit, a, 1);
    o();


    return 0;
}

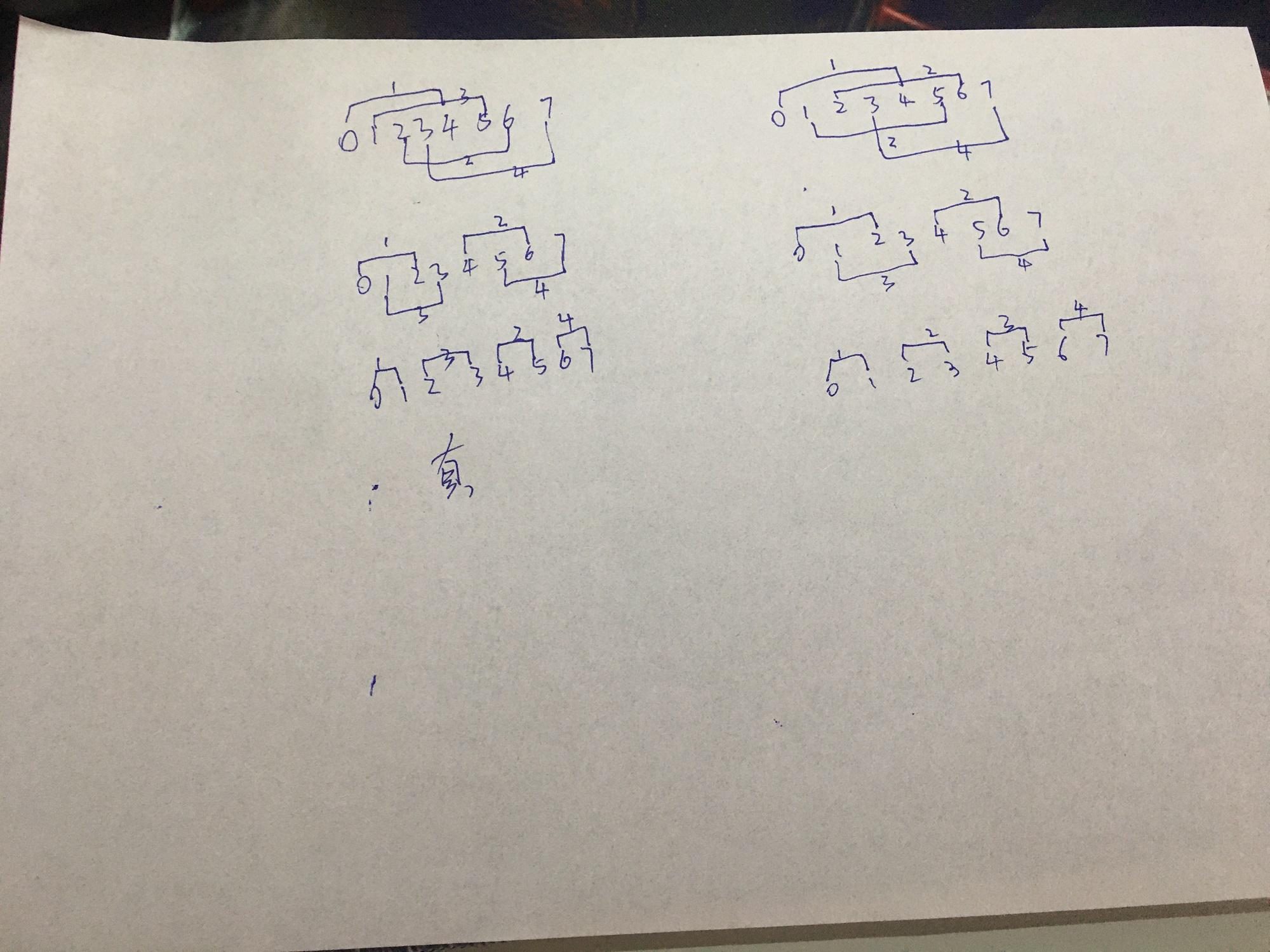
可能有助于理解的三张手稿：