最长公共子序列

我个人是不太喜欢用这个oj的，我dev上的代码他不能跑，我觉得不对的代码他却能跑....

题目

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

输入：text1 = "abcde", text2 = "ace"
输出：3

解释：最长公共子序列是 "ace"，它的长度为 3。

示例 2:

输入：text1 = "abc", text2 = "abc"
输出：3

解释：最长公共子序列是 "abc"，它的长度为 3。

示例 3:

输入：text1 = "abc", text2 = "def"
输出：0

解释：两个字符串没有公共子序列，返回 0。

提示:

1 <= text1.length <= 1000 1 <= text2.length <= 1000 输入的字符串只含有小写英文字符。

我们就那第一个例子来思考

直接思考abcde和ace的话，那么我们可能要思考他们两个人所有可能的子串，然后一一对比，找到最长的，但一想

假如一个字符串的长度是n，那么子串的长度可能是从1到n，设子串的长度为k，长度为k的字串的个数就是$c_n^k$

字串的个数是$sum = c_n^1+c_n^2+c_n^1+...+c_n^n$

就是$(1+x)^n$展开式的系数-1，令x=1，就是$2^n-1$

所以找到所有的字串是不现实的。

所以需要将大问题化为一个个小问题解决，将大问题化为小问题的方法有分治，动规，带记忆的递归等。

分治想这题的话，我认为是将第二个字符串分治，将第二个字符串分成两段，计算第一段和第一个字符串的最长公共子序列，然后计算第二段和第一个字符串的最长公共子序列，再将二者答案合并，但是合并这两部分的答案我想不出怎么合并。

动规的话就是定义状态，常见的就是定义dp[i][j]为考虑第一个字符串的前i个字符，考虑第二个字符串的前j个字符，最长的公共子序列长度为dp[i][j].

那么状态转移方程为：

$$ dp[i][j]= \begin{cases} dp[i-1][j-1]+1,& str1[i]==str2[j]\\ max(dp[i-1][j], dp[i][j-1]),& str1[i]!=str2[j] \end{cases} $$

解释：

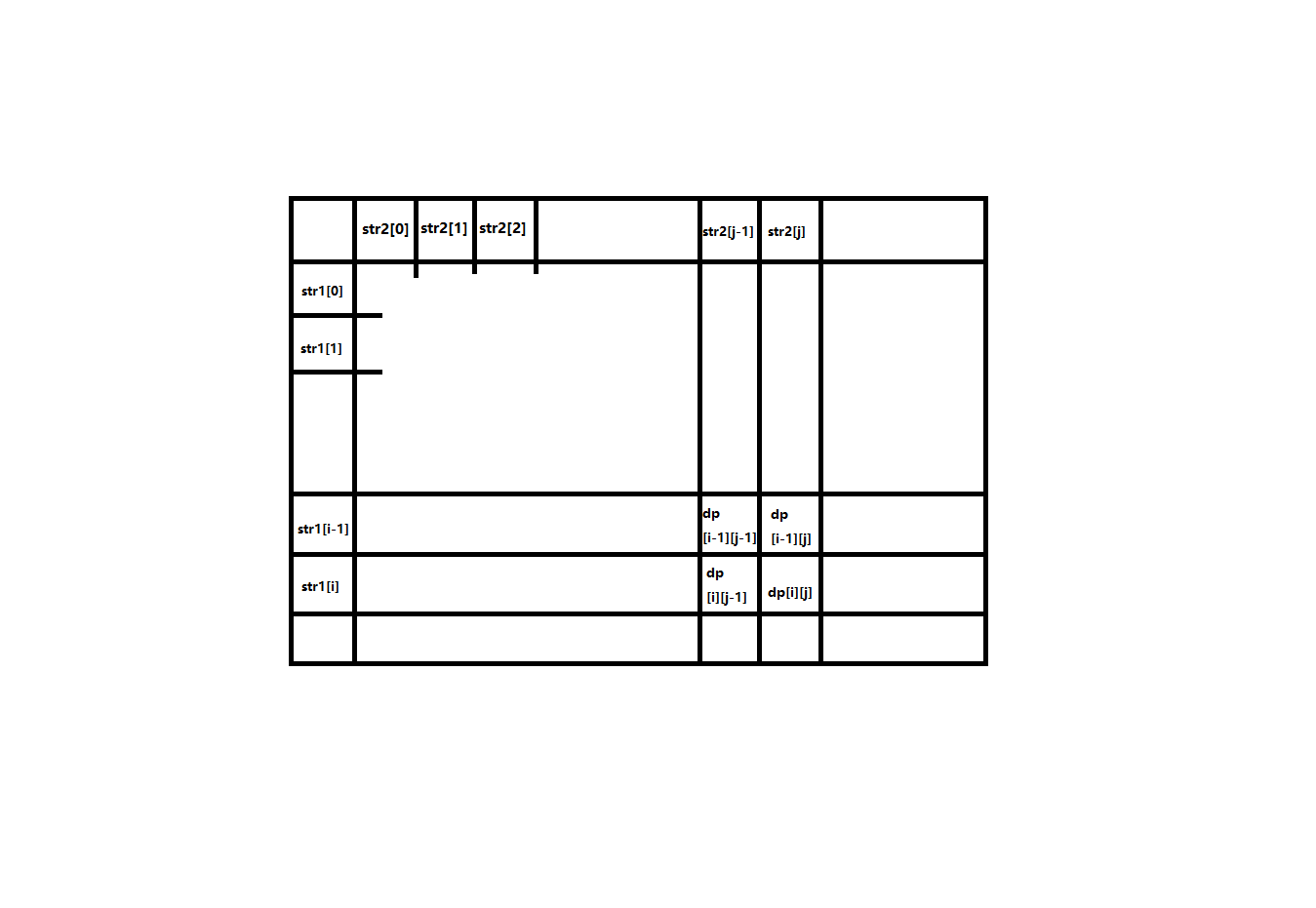
看图吧